今回はPythonのnumpyモジュールの使い方を初心者向けに解説していきます。
Pythonのnumpyは、データ処理や科学技術計算において必須のライブラリとして広く利用されています。
特に初心者にとってはnumpyの基本的な文法を理解することが重要です。
本記事では初心者がnumpyを効果的に活用するために最低限知っておきたい文法に焦点を当てます。
array、arange、eye、zeros、ones、dot、cross、trace、linalg、そしてrandomなどの関数やメソッドを通じて、どのようにしてnumpyを使いこなすかを解説していきます。
numpyのパワフルな機能を理解し、Pythonでのデータ処理をより効率的に行うための基礎を築くためにぜひこの記事をお読みください。
PythonでNumpyを使う方法
Numpyはサードパーティ製のライブラリなのでインポート文を書くだけでは使用できません。
ターミナルで以下のコマンドを実行してプロジェクトにインストールしておく必要があります。
pip install numpyimport numpyPythonのNumpyでベクトルを作成、操作する方法
Numpyはリストとは違うndarrayと言うタイプのデータを扱うもので、主にベクトルか行列を操作する時に使います。
例えばベクトルを作成するには以下のようにarangeメソッドを使うことになります。
第一引数に最小の数字、第二引数に最大の数字、第三引数に数字の間隔を指定します。
import numpy
# 1以上6未満を1ずつの間隔で作る
row_column = numpy.arange(1,6,1)
print(row_column) # [1 2 3 4 5]と表示される
# 1以上6未満を2ずつの間隔で作る
row_column = numpy.arange(1,6,2)
print(row_column) # [1 3 5]と表示される表示結果がリストに似ていますがリストは要素同士を「,」で挟んで表現しますが、Numpyが作成するndarrayと言うデータは要素同士を記号で挟みません。
# リスト
[1,2,3]
# Numpyが扱うndarray
[1 2 3]一方でndarrayもリストのように要素をインデックス番号で指定することで取得できます。
import numpy
# 1以上6未満を1ずつの間隔で作る
row_column = numpy.arange(1,6,1)
print(row_column) # [1 2 3 4 5]と表示される
print(row_column[0]) # 1と表示されるまたデフォルトだと上記コードのように整数で数字を表現しますが、小数点で表現するにはarangeメソッドの第四引数にdtype=numpy.float64を追加します。
import numpy
# 1以上6未満を1ずつの間隔で作る
row_column = numpy.arange(1,6,1, dtype=numpy.float64)
print(row_column) # [1. 2. 3. 4. 5.]と表示されるちなみに中身の要素に同じ処理をしたい時にはfor文を使わなくても専用のメソッドが用意されているのがndarrayのもう一つの特徴です。
import numpy
row_column = numpy.arange(1,6,1)
# 行列の各要素に関数を実行する(for文が不要)
# 1を加算
print(numpy.add(test,1)) # [2 3 4 5 6]と表示される
# 2乗する
print(numpy.square(test)) # [1 4 9 16 25]と表示されるベクトルの作成にはarrayメソッドを使う方法もあり、こちらの方が直感的に書くことができます。
import numpy
a = numpy.array([1,2,3])
print(a) # [1 2 3]と表示される
b = numpy.array([4,5,6])
print(b) # [4 5 6]と表示される数学に登場するようなベクトル同士の和と差は四則演算の記号をそのまま使えます。
import numpy
a = numpy.array([1,2,3])
print(a) # [1 2 3]と表示される
b = numpy.array([4,5,6])
print(b) # [4 5 6]と表示される
# 足し算
add_result = a + b
print(add_result) # [5 7 9]と表示される
# 引き算
sub_result = b - a
print(sub_result) # [3 3 3]と表示されるまた内積と外戚については専用のメソッドが用意されています。
import numpy
a = numpy.array([1,2,3])
print(a) # [1 2 3]と表示される
b = numpy.array([4,5,6])
print(b) # [4 5 6]と表示される
# 内積
inner_result = numpy.dot(a,b)
print(inner_result) # 32と表示される
# 外積
cross_result = numpy.cross(a,b)
print(cross_result) # [-3 6 -3]と表示されるPythonのNumpyで行列を作成、操作する方法
前章では1次元のndarryであるベクトルでしたが、arrayメソッドというものでndarrayを二次元にすることで行列になります。
import numpy
# ndarrayを2次元配列のように書くと行列になる
test = numpy.array([[1,2,3],[4,5,6]])
print(test)
#[[1 2 3]
[4 5 6]]と表示される二次元なので要素の取得にも2階層でインデックス番号を指定することになりますので、入れ子のリストと同じような形です。
import numpy
test = numpy.array([[1,2,3],[4,5,6]])
# 0行0列の値
print(test[0,0]) # 1が表示される
# 1行2列の値
print(test[1,2]) # 6が表示される またリストのスライスのように特定の範囲で切り取ることも可能です。
import numpy
test = numpy.array([[1,2,3],[4,5,6]])
# スライス(エクセルのように特定の範囲で切り取る)
print(test[0:2,0:2])
# [[1 2]
[4 5]]と表示される特徴的な行列である、単位行列、0行列、三角行列、全てが1の行列についてはそれぞれ専用のメソッドを使うことで作成できます。
注意点としては特徴的な行列になるとデフォルトで小数点表示になりますので、整数にしたいときはメソッドの第四引数でdtype=numpy.int64を追加しておきます。
import numpy
# 特徴的な行列(デフォルトが小数点なので整数であればdtype=int64を第二引数に指定)
# 単位行列
print(numpy.eye(6, dtype=numpy.int64))
[[1 0 0 0 0 0]
[0 1 0 0 0 0]
[0 0 1 0 0 0]
[0 0 0 1 0 0]
[0 0 0 0 1 0]
[0 0 0 0 0 1]]
# ゼロ行列(第一引数はタプル型)
print(numpy.zeros((3,3), dtype=numpy.int64))
[[0 0 0]
[0 0 0]
[0 0 0]]
# 三角行列
print(numpy.tri(4, dtype=numpy.int64))
[[1 0 0 0]
[1 1 0 0]
[1 1 1 0]
[1 1 1 1]]
# 全ての要素が1の行列
print(numpy.ones((3,3), dtype=numpy.int64))
[[1 1 1]
[1 1 1]
[1 1 1]]前章でやった和と差、内積と外積については行列についても同じ記号とメソッドで実行できます。
import numpy
a = numpy.array([[1,2,3],[4,5,6],[7,8,9]])
b = numpy.array([[10,11,12],[13,14,15],[16,17,18]])
# 足し算
print(a + b)
#[[11 13 15]
[17 19 21]
[23 25 27]]と表示される
# 引き算
print(b - a)
#[[9 9 9]
[9 9 9]
[9 9 9]]と表示される
# 内積
print(numpy.dot(a,b))
#[[ 84 90 96]
[201 216 231]
[318 342 366]]と表示される
# 外積
print(numpy.cross(a,b))
#[[-9 18 -9]
[-9 18 -9]
[-9 18 -9]]と表示されるまたベクトルと違って行列は2次元の構成のために転置、トレースという計算もあります。
import numpy
c = numpy.array([[1,2],[3,4]])
# 転置
print(c.T)
#[[1 3]
[2 4]]と表示される
# トレース(対角成分の和)
print(c.trace())
# 5と表示されるPythonのNumpyを使った特殊な計算
Numpyはndarrayと言うデータを扱うためベクトルと行列が主な使用目的になりますが、実は別の計算にもNumpyのメソッドが活用できる場面があります。
例えば連立一次方程式です。
x + 2y = 4
2x + 3y = 5
と言う計算を行列に見立てることで計算することができます。
2つの式をそれぞれarrayメソッドを使ってndarrayとして作成し、linalog.solveと言う線形代数に使用するメソッドの第一引数、第二引数にそれぞれのndarrayを入れるようにします。
結果もndarrayになるのですが、0番目の要素がxの値で1番目の要素がyの値になります。
import numpy
# 連立一方程式
# x + 2y = 4
# 2x + 3y = 5
#左辺
left_val = numpy.array([[1,2],[2,3]])
#右辺
right_val = numpy.array([4,5])
result = numpy.linalg.solve(left_val, right_val)
print(result) # [-2. 3.]と表示される x=-2,y=3と言う意味もう一つの使い道は乱数の生成です。
random.randと言うメソッドがあり引数に入れた数字の数だけランダムな小数点の数を生成します。
import numpy
num = numpy.random.rand(10)
print(num)
[0.21295215 0.60622425 0.19667102 0.08954446 0.71169397 0.55212261
0.40356416 0.26672818 0.01232888 0.03525164]さらにrandom.normalとすることで正規分布の乱数を生成できます。
第一引数に要素の数、第二引数に平均値、第三引数に標準偏差を指定します。
import numpy
test = numpy.random.normal(3, 4, 10)
print(test)
[ 2.04460854 1.26339194 8.17363989 3.69989822 3.51994054 8.79206851
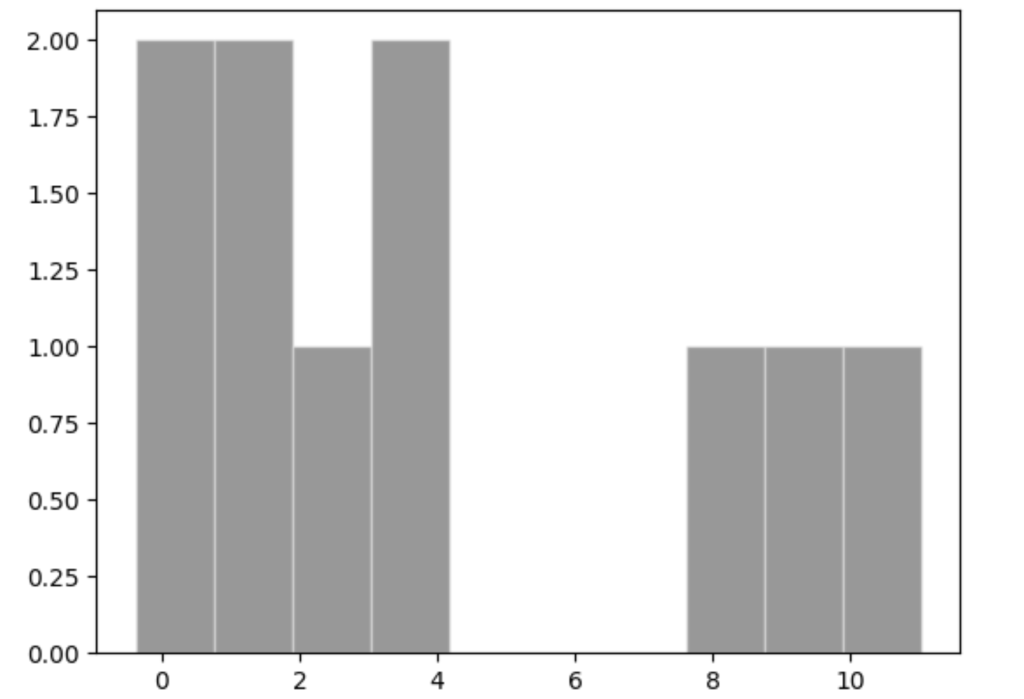
-0.37635098 -0.13886475 1.39870029 11.03507545]これをmatplotlibと言う別のモジュールを使ってグラフにできます。
matplotlibもサードパーティ製のモジュールなのでインストールが必要です。
pip install matplotlibimport numpy
#ここを追加
import matplotlib.pyplot as plt
test = numpy.random.normal(3, 4, 10)
#ここを変更
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.hist(test, bins=10, color="#333", ec="#eee", alpha=0.5)
plt.show()