「Pythonを使って初心者でもグラフを作成する方法があれば知りたい」
「Matplotlibを使ってグラフを作成しているけど軸の数値範囲を設定する方法がわからない」
「Matplotlibを使って複数のグラフを同時に表示する方法が知りたい」
本日はそんな方に向けてPythonのMatplotlibライブラリを使ったグラフの作成について解説していきます。
PythonのMatplotlibは、データ可視化のための強力なツールであり初心者からプロまで幅広いユーザーに利用されています。
本記事ではMatplotlibを使用してグラフを作成する方法を詳しく解説します。
Figureの作成からsubplotの配置、scatterプロットの描画、グリッドの追加、そしてタイトルや軸ラベルの設定まで、基本的な機能を網羅的に説明していきます。
これによりMatplotlibを使ってデータを視覚的に表現する方法を理解し、自分のプロジェクトや解析に活用できるようになるでしょう。
また動画もあるので必要に応じて活用してください。
PythonでMatplotlibを使ってグラフを作成する方法
Matplotlibはサードパーティ製のライブラリなのでインストールしてからじゃないと使用できません。
pip install matplotlibインストールが完了したらMatplotlibのpyplotというクラスをインポートします。
また名前が少々長いのでasを使って「plt」と省略して使うことが多いです。
import matplotlib.pyplot as pltグラフを作成する基本の手順は以下のとおりです。
・画面を作成
・軸を作成
・データを点で配置
・グラフの表示
それぞれをコードにすると以下のようになります。
import matplotlib.pyplot as plt
# 画面を作成
fig = plt.figure()
# 軸を作成
ax1 = fig.add_subplot(1,1,1)
# データを点で配置
x = [0,1,2]
y = [0,1,2]
ax1.plot(x,y)
# グラフの表示
plt.show()
こちらを実行すると以下のように一次関数のグラフが作成できます。
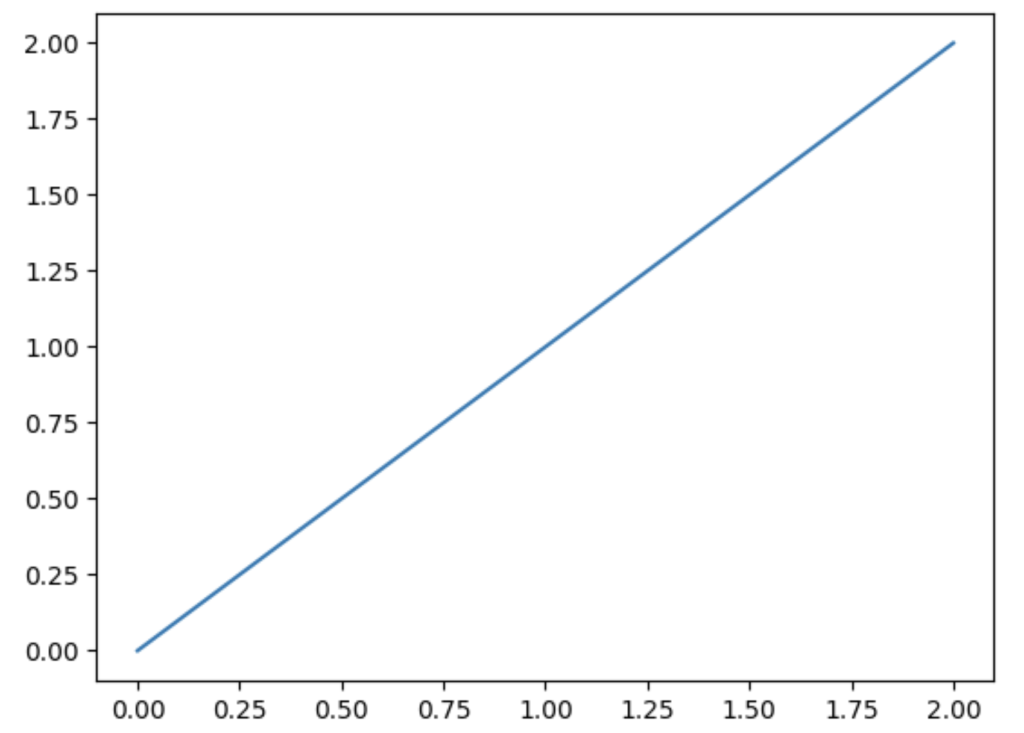
ちなみにyの値をxの乗数にすることで二次関数になります。
import matplotlib.pyplot as plt
import numpy
x = numpy.linspace(0, 5, 100)
y = x ** 2
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(x, y, "-")
plt.show()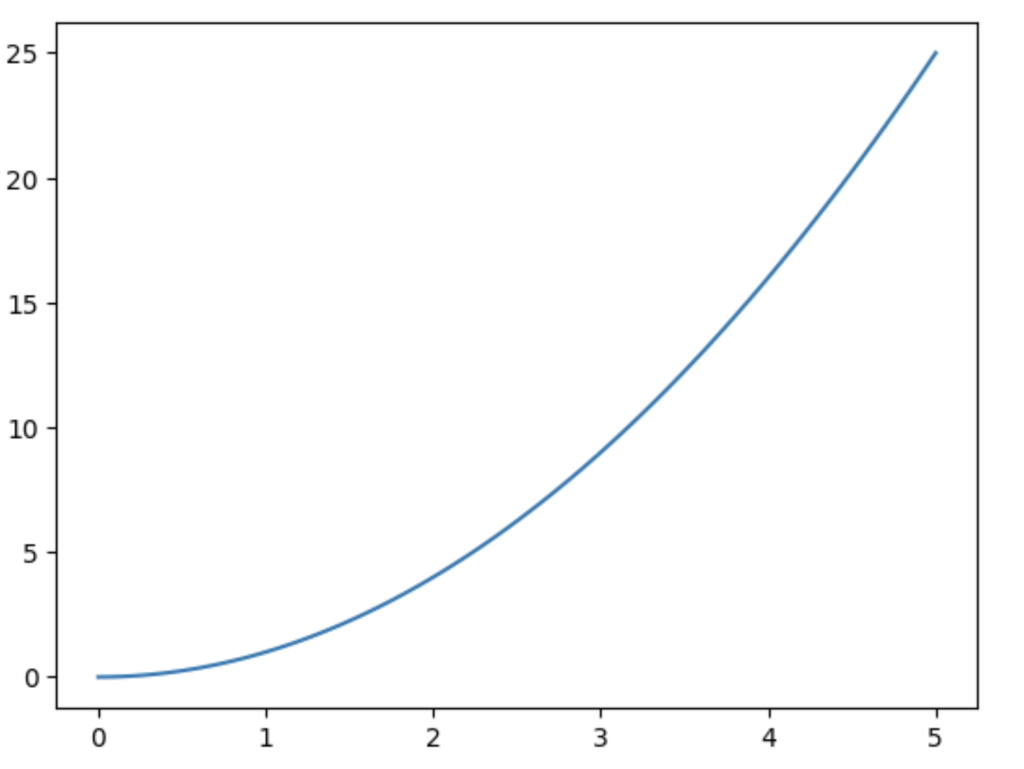
もう一度、一次関数を例題にして解説をしていきますが、線を2本にしたいときはそれぞれのデータを用意してplotメソッドを実行すればOKです。
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
x1 = [0,8,16]
y1 = [0,8,16]
ax.plot(x1,y1)
x2 = [0,2,4]
y2 = [0,4,16]
ax.plot(x2,y2)
plt.show()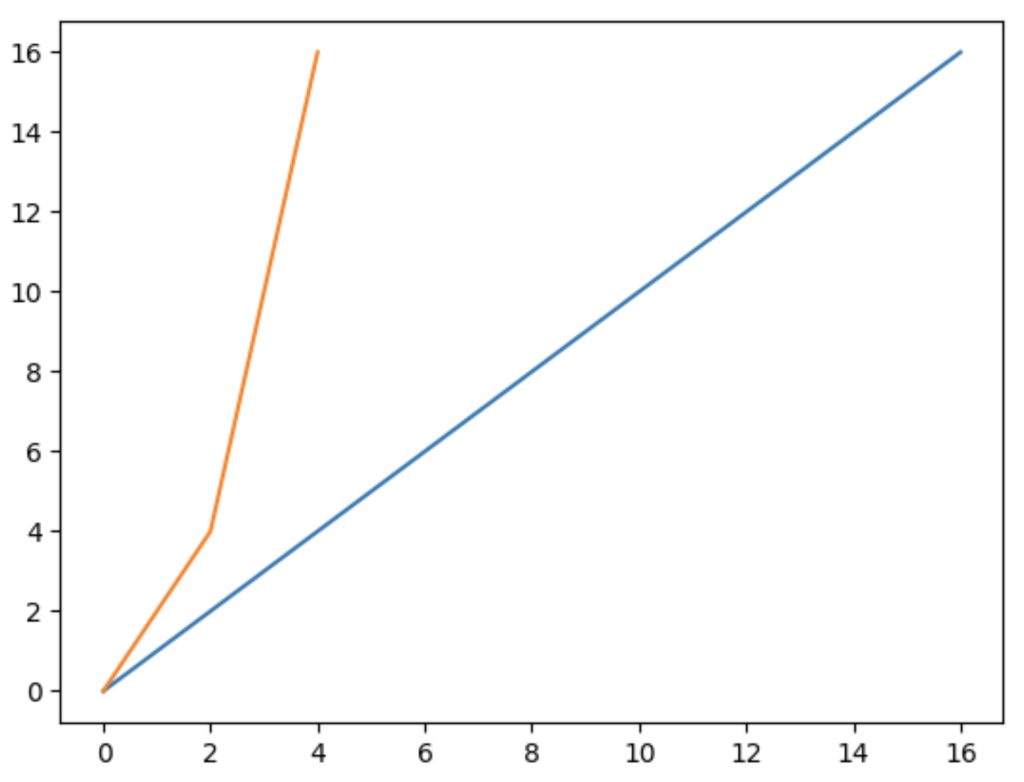
また値を見やすくするためにgridというメソッドで目盛をグラフに追加できます。
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
x1 = [0,8,16]
y1 = [0,8,16]
ax.plot(x1,y1)
x2 = [0,2,4]
y2 = [0,4,16]
ax.plot(x2,y2)
# ここを追加
ax.grid(True)
plt.show()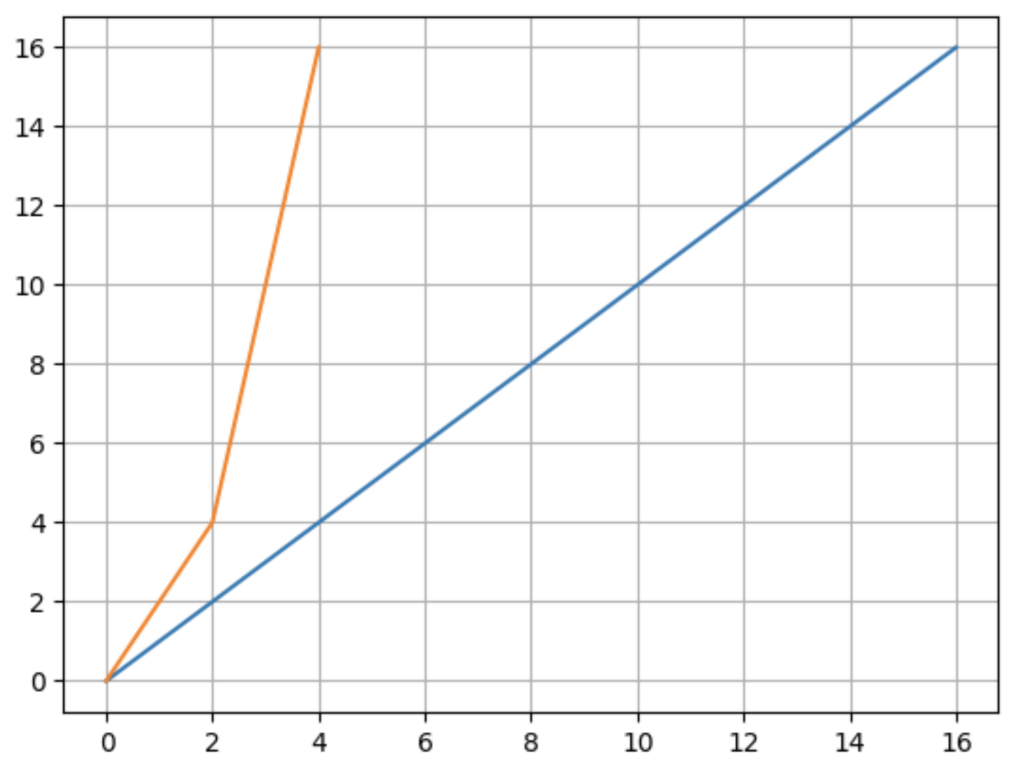
線を複数にするときは上記のように同じグラフに混在させる方法と、もう一つはグラフ自体を複数にする方法があります。
add_subplotメソッドが軸、つまりグラフの作成を担っています。
add_subplot(a,b,c)という3つの引数で、「画面をa:bに分割してc番目に軸を設定する」という意味になります。
import matplotlib.pyplot as plt
fig = plt.figure()
# figureを2:1に分割して1番目に軸を配置する
ax1 = fig.add_subplot(2,1,1)
# figureを2:1に分割して2番目に軸を配置する
ax2 = fig.add_subplot(2,1,2)
x1 = [0,1,2]
y1 = [0,1,2]
ax1.plot(x1,y1)
x2 = [1,5,10]
y2 = [3,3,3]
ax2.plot(x2,y2)
plt.show()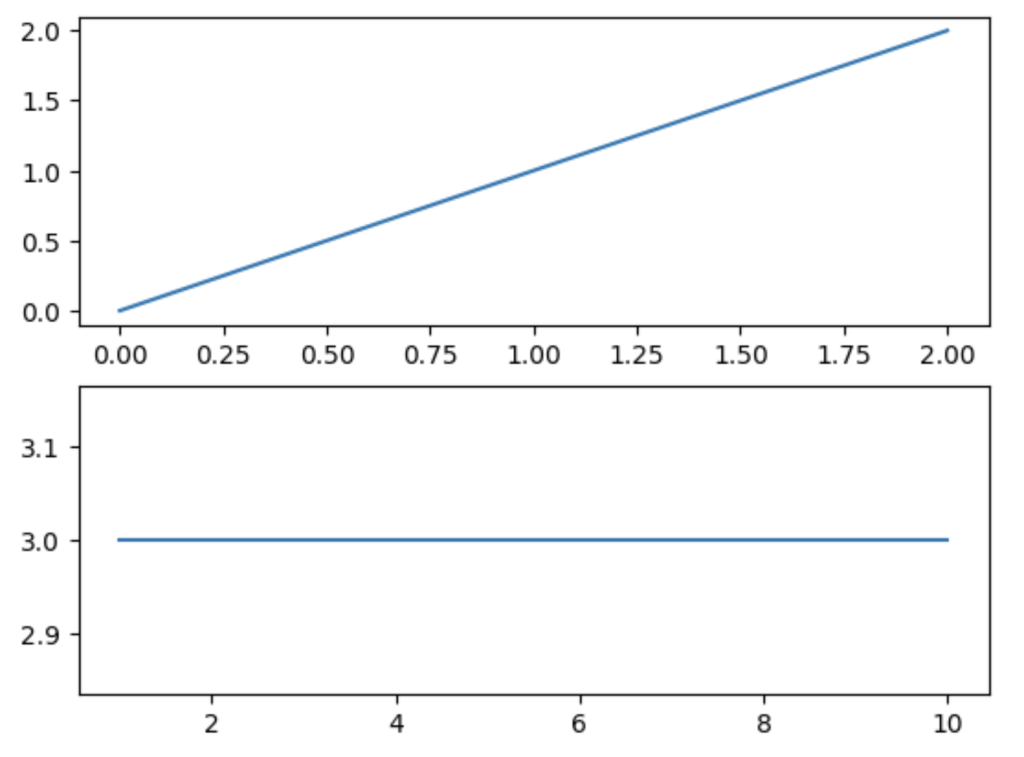
グラフを分割して増やしたときはset_titleというメソッドでタイトルをつけることが多いです。
import matplotlib.pyplot as plt
fig = plt.figure()
ax1 = fig.add_subplot(2,1,1)
# ここを追加
ax1.set_title("graph1")
ax2 = fig.add_subplot(2,1,2)
# ここを追加
ax1.set_title("graph2")
x1 = [0,1,2]
y1 = [0,1,2]
ax1.plot(x1,y1)
x2 = [1,5,10]
y2 = [3,3,3]
ax2.plot(x2,y2)
plt.show()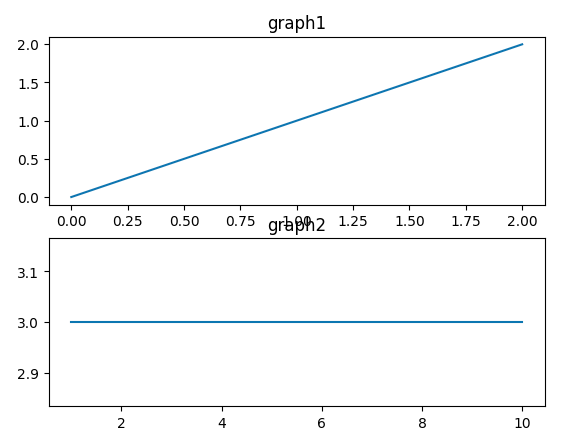
またグラフの軸の数値範囲を設定したいときはset_xlimとset_ylimというメソッドを使います。
set_xlimはx軸の範囲を決めるもので、引数はleftが最小値でrightが最大値になります。
set_ylimはy軸の範囲を決めるもので、引数はbottomが最小値でtopが最大値になります。
さらにset_xlabelでx軸のラベルを、set_ylabelでy軸のラベルも追加できます。
線のラベルはlegendというメソッドがあり、第一引数から順番に作成したラベル名を文字列で記載します。
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
x1 = [0,4,8,12,16,20]
y1 = [0,8,16,24,32,40]
ax.plot(x1,y1)
x2 = [0,2,4,6,8,10,12,14,16,18,20]
y2 = [0,2,4,6,8,10,12,14,16,18,20]
ax.plot(x2,y2)
# グリッド線をオンにする
ax.grid(True)
# x軸の範囲
ax.set_xlim(left=0, right=20)
# y軸の範囲
ax.set_ylim(bottom=0, top=40)
# x軸のラベル
ax.set_xlabel("speed")
# y軸のラベル
ax.set_ylabel("km")
# グラフのタイトル
ax.set_title("sample image")
# グラフのラベル
ax.legend(["f(x)=2x", "f(x)=x"])
plt.show()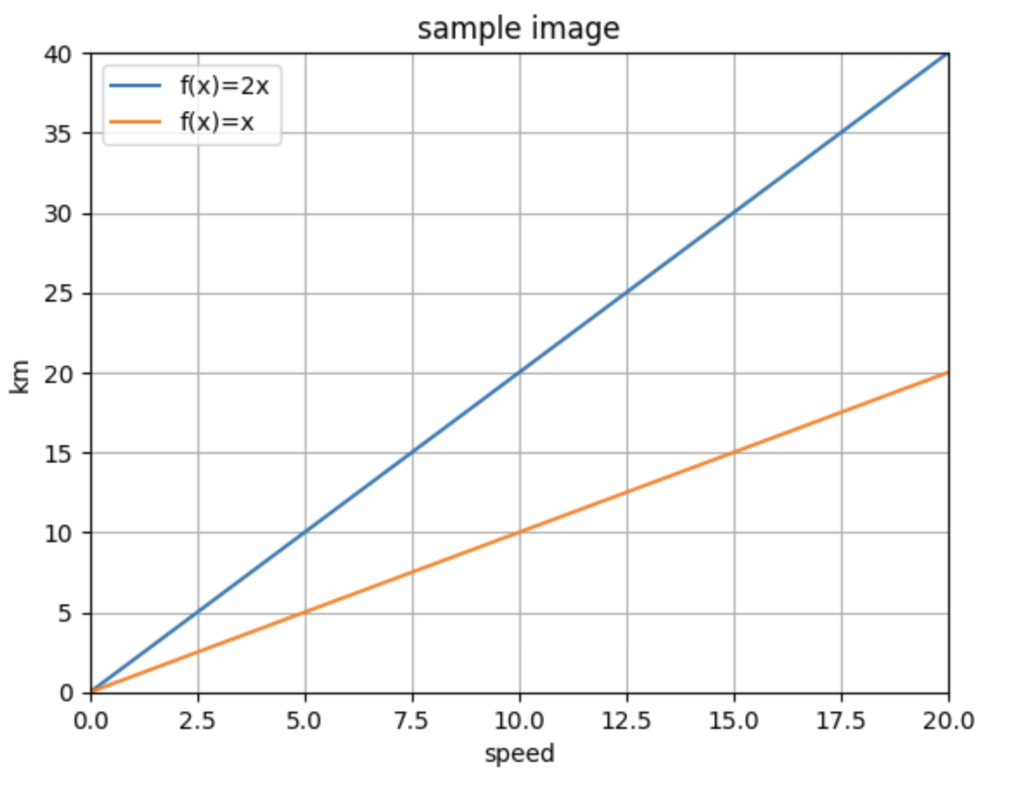
Pythonのseabornを使ってmatplotlibで作るグラフに色をつける
現状のグラフでも問題ないですがseabornというライブラリを併用することでデザインをすることができます。
seabornもmatplotlibと同じくサードパーティ製のライブラリですのでインストールが必要です。
pip install seabornseabornにはsetメソッドがあり引数のstyleというパラメーターに指定のキーワードを指定することができます。
style=”dark”とすると以下のようなグラフになります。
import matplotlib.pyplot as plt
import seaborn
seaborn.set(style="dark")
plt.plot([0,10,20],[0,50,100])
plt.show()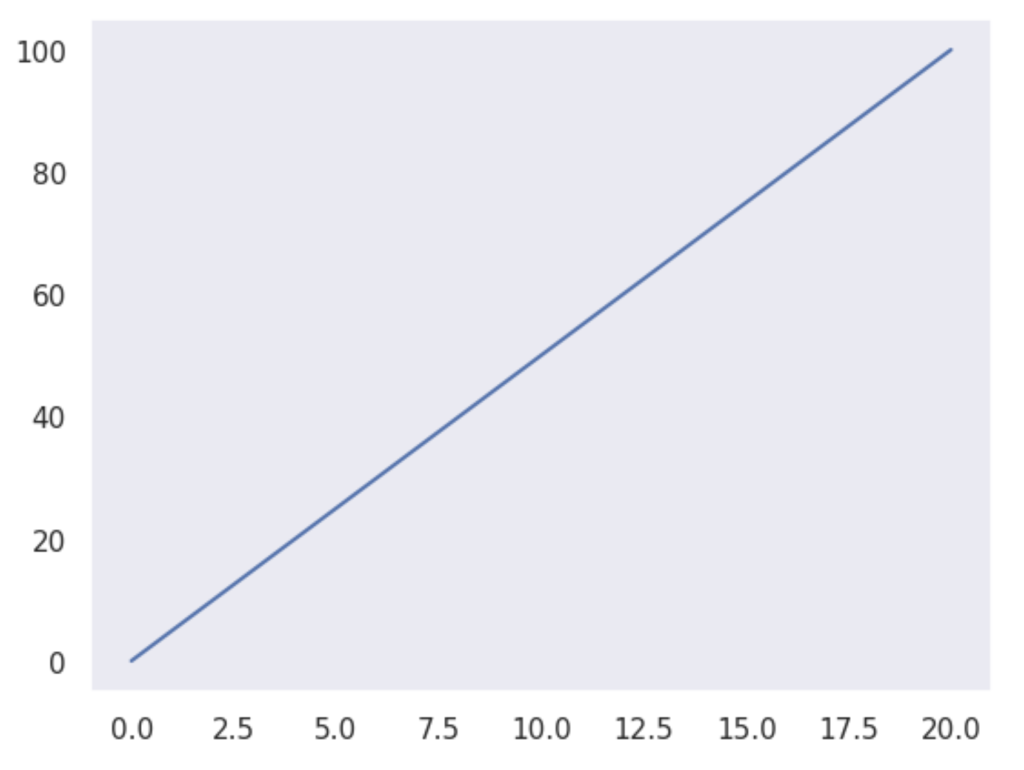
逆にstyle=”white”とすると今まで通りの白背景の見た目になります。
import matplotlib.pyplot as plt
import seaborn
# ここを修正
seaborn.set(style="white")
plt.plot([0,10,20],[0,50,100])
plt.show()
またstyle=”darkgrid”とすると目盛を加えることも可能です。
import matplotlib.pyplot as plt
import seaborn
# ここを修正
seaborn.set(style="darkgrid")
plt.plot([0,10,20],[0,50,100])
plt.show()
PythonのMatplotlibで色んなパターンのグラフや図を作成する
前章ではシンプルな一次関数のグラフでしたがMatplotlibではいろんな種類のグラフを作成できます。
資料や論文など使用する場所によって見せ方を変えることはよくあるので色んなパターンを練習しておきましょう。
PythonのMatplotlibで散布図を作成する
例えば散布図を作成したいときはNumpyを追加でインストールします。
!pip install numpy続いてNumpyをインポートした上で、ランダムな数字を作成します。
Numpyで作成された乱数をMatplotlibのscatterというメソッドで散布図にすることができます。
import matplotlib.pyplot as plt
import numpy
x = numpy.random.rand(10)
y = numpy.random.rand(10)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# xの値、yの値、点の大きさ、点の透明度、点の太さ、マーカーの形、マーカーの色
ax.scatter(x,y,s=100, alpha=1, linewidths=1, marker="+",c="#666")
plt.show()
scatterメソッドを2個に分けて実行することで一度に2個の散布図を作成することも可能です。
ただし散布図はバラバラの点なので通常のグラフよりも見た目に気を遣って見分けがつくようにすることが求められます。
import matplotlib.pyplot as plt
import numpy
x1 = numpy.random.rand(10)
y1 = numpy.random.rand(10)
x2 = numpy.random.rand(10)
y2 = numpy.random.rand(10)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# xの値、yの値、点の大きさ、点の透明度、点の太さ、マーカーの形、マーカーの色
ax.scatter(x1, y1, s=50, alpha=1, linewidths=1, marker="X",c="c")
ax.scatter(x2, y2, s=50, alpha=1, linewidths=1, marker="D",c="y")
plt.show()
相関値の計算はpandasのcorrメソッドがあり、データフレームにcorrメソッドを実行することで-1から1の間で計算ができます。
プラスマイナス関わらず0に近づくにつれて相関が薄い(xとyに関係性が薄い)ということになります。
データを新しく変数dataとして辞書にして用意してみました。
こちらのdataをデータフレームに変換した後でcorrメソッドを実行して相関値を求めます。
データフレームに変換するためにpandasが必要なのでインストールしてから実行します。
!pip install pandasimport matplotlib.pyplot as plt
import pandas
data = {
"x": [100, 76, 55, 45, 98],
"y": [47, 36, 90, 100, 24]
}
df = pandas.DataFrame(data)
corr = df.corr()["x"]["y"]
print(f"xとyの関連度合いは{corr}です")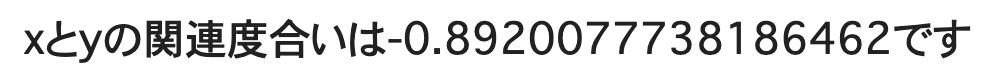
-0.89ということで負の相関が強いことがわかりました、xが増えればyが減っていく法則性が見られたわけですね。
相関値を出すことで散布図をグラフとして見なくても2つのデータの関連度合いを数字として把握することができます。
相関値は正規直線からの距離を元に計算されます。
正規直線とは「相関値1もしくは-1という、正か負の相関が完全にあった時にデータがとる直線の並び」のことでデータの理想系という具合です。
正規直線をもとに視覚的に相関を知りたい時には散布図の中に表示させることで確認できます。
また散布図に正規直線を表示させるにはseabornというサードパーティ製のライブラリを使用します。
!pip install seabornseabornライブラリにあるreglotというメソッドを使うことで正規直線を作成できます。
regplotは第一引数に散布図に使用したデータフレーム、第二引数にxの値、第三引数にyの値、第四引数に正規直線の色を設定します。
import matplotlib.pyplot as plt
import pandas
import seaborn
data = {
"x": [100, 76, 55, 45, 98],
"y": [47, 36, 90, 100, 24]
}
df = pandas.DataFrame(data)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x=df["x"], y=df["y"], alpha=1, linewidths=1, marker="+",c="#666")
# 回帰直線を作る。データフレーム、x軸の値、y軸の値、色
seaborn.regplot(data=df, x=df["x"], y=df["y"], line_kws={"color": "red"})
plt.show()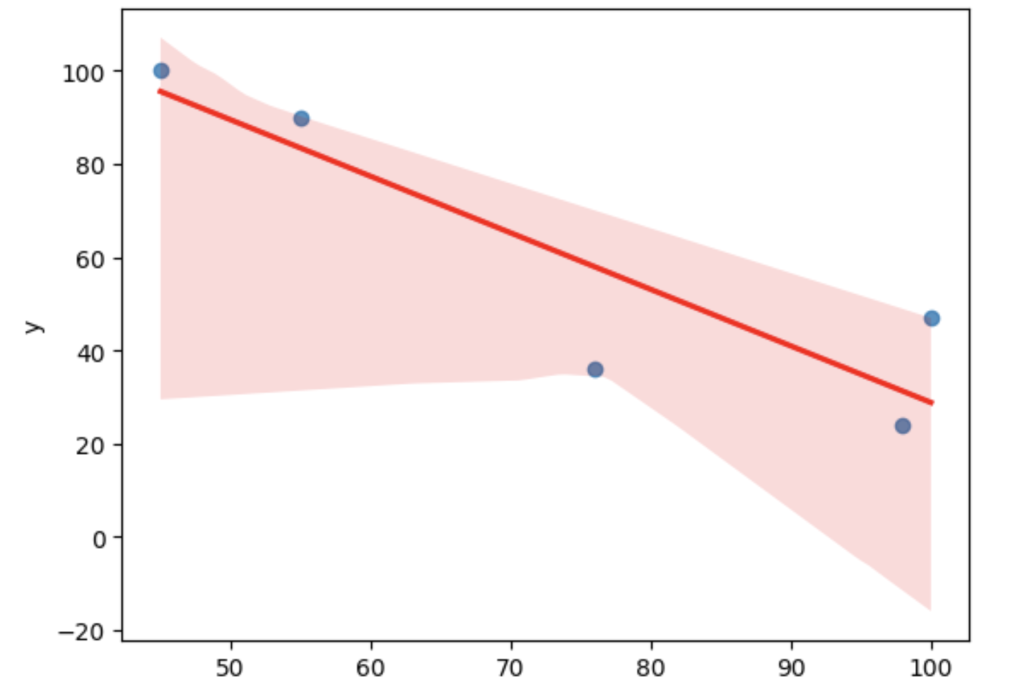
上図の赤い直線が正規直線です。
今回のデータは負の相関ですので相関値-1だったときのデータの配置を線にして表現するのが正規直線です。
各データのプロット位置と正規直線からの距離を持って相関度合いを確認するわけですね。
通常のグラフだと本記事で色々と紹介している通りmatplotlibを使えば大体のグラフは表示できるのですが、このようなグラフのカスタマイズにseabornを使うことになります。
例えばjointplotというメソッドを使うと正規直線と散布図とヒストグラムを同時に表示することが可能です。
import matplotlib.pyplot as plt
import pandas
import seaborn
data = {
"x": [100, 76, 55, 45, 98],
"y": [47, 36, 90, 100, 24]
}
df = pandas.DataFrame(data)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x=df["x"], y=df["y"], alpha=1, linewidths=1, marker="+",c="#666")
# ここを修正
# ヒストグラム付きの回帰直線を作る。データフレーム、x軸の値、y軸の値、プロットの種類、色
seaborn.jointplot(data=df, x=df["x"], y=df["y"], kind="reg", line_kws={"color": "red"})
plt.show()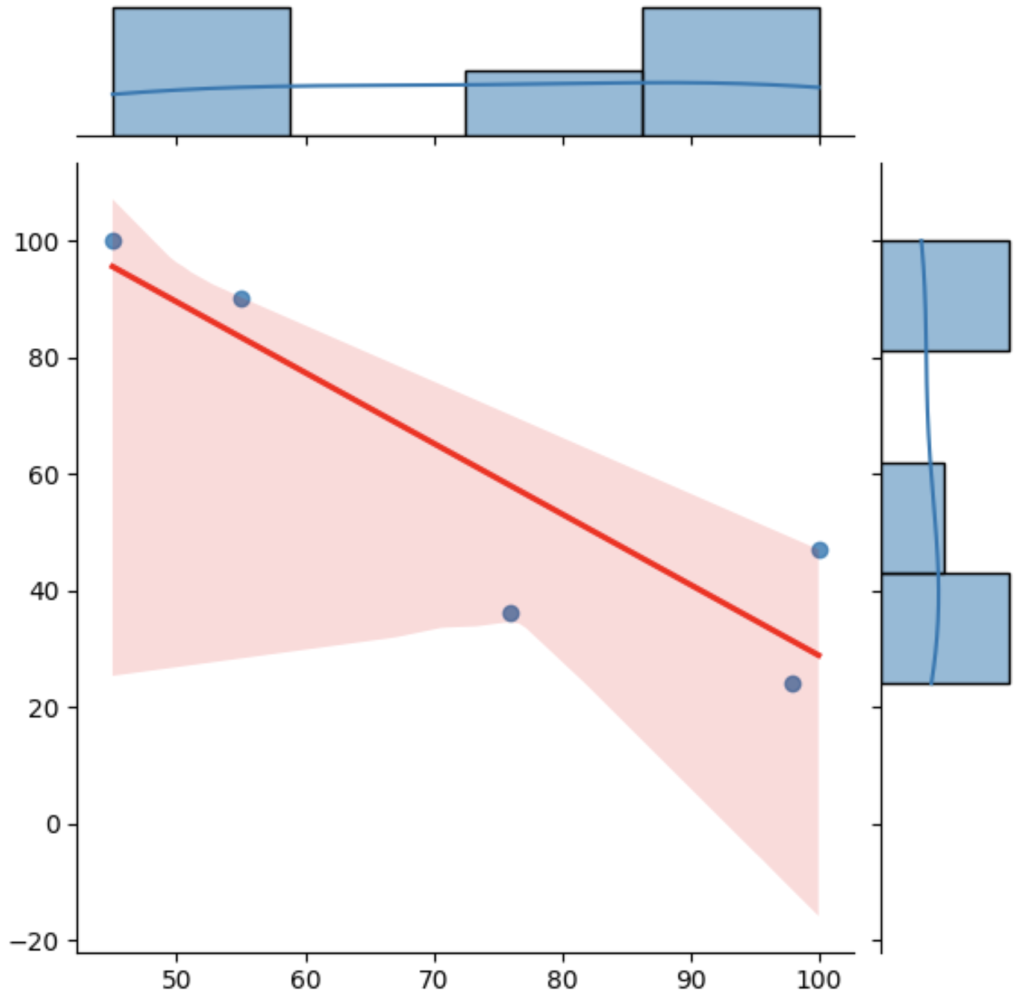
他にはheatmapというメソッドで相関度合いをヒートマップ形式にして表示することもできます。
import matplotlib.pyplot as plt
import pandas
import seaborn
data = {
"x": [100, 76, 55, 45, 98],
"y": [47, 36, 90, 100, 24]
}
df = pandas.DataFrame(data)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x=df["x"], y=df["y"], alpha=1, linewidths=1, marker="+",c="#666")
# ここから変更
# 相関値
corr = df.corr()
# ヒートマップを作る。相関値、相関値を一緒に表示させるか、最大値、最小値、中央の相関なし
seaborn.heatmap(corr, annot=True, vmax=1, vmin=-1, center=0)
plt.show()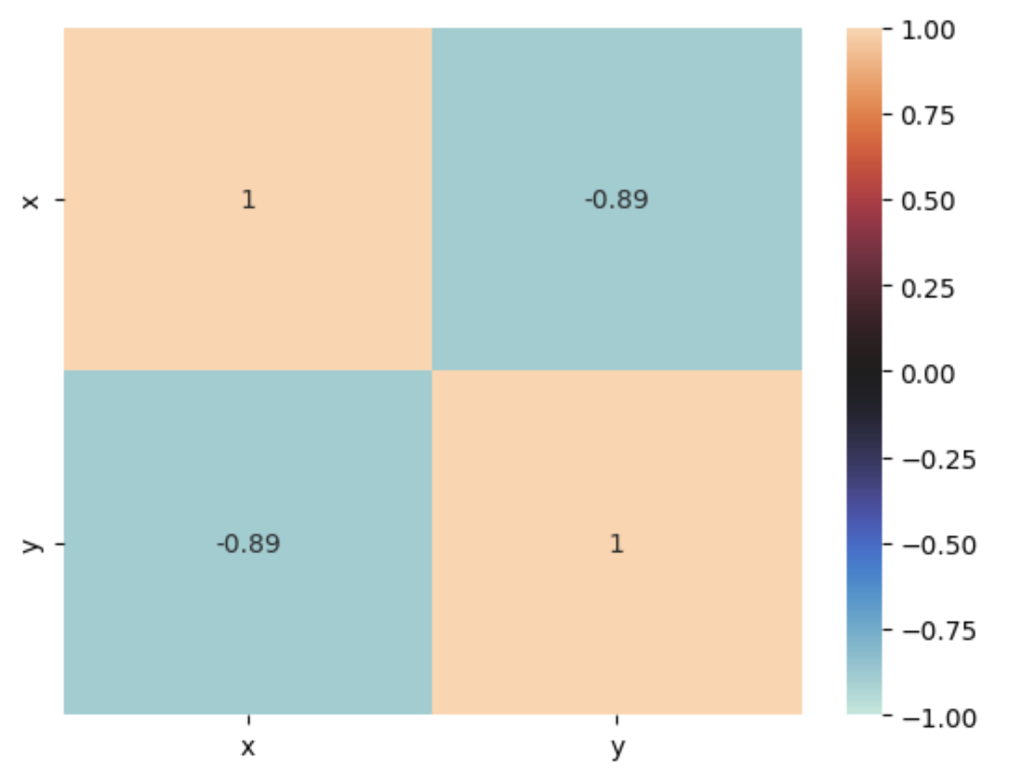
さらにpairplotというメソッドを使うとヒストグラムと散布図を使った散布図行列という別の表示形式に変更することもできます。
import matplotlib.pyplot as plt
import pandas
import seaborn
data = {
"x": [100, 76, 55, 45, 98],
"y": [47, 36, 90, 100, 24]
}
df = pandas.DataFrame(data)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x=df["x"], y=df["y"], alpha=1, linewidths=1, marker="+",c="#666")
# ここから変更
# 散布図行列を作る。
seaborn.pairplot(data=df, kind="reg")
plt.show()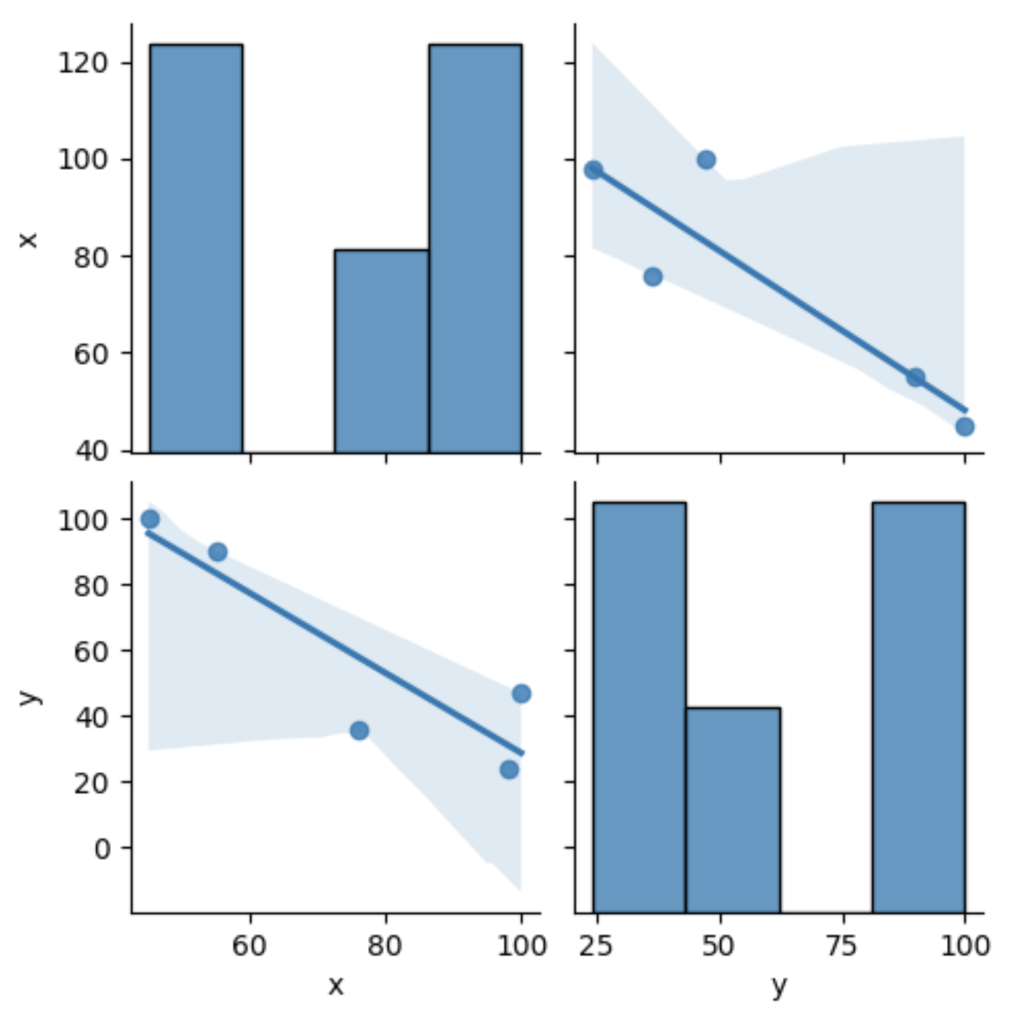
PythonのMatplotlibで棒グラフを作成する方法
続いては棒グラフになります。
barというメソッドがあり、第一引数にxの値、第二引数にyの値、第三引数にwidthというキーワードで棒の太さ、第四引数にlinewidthというキーワードで枠線の太さ、第五引数にedgecolorというキーワードで枠線の色を設定します。
import matplotlib.pyplot as plt
label = ["a", "b", "c"]
x = ["J","F","M"]
y = [100,200,300]
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# x軸、y軸、棒の太さ(1が基準)、枠線の太さ、枠線の色
ax.bar(x, y, width=0.4, linewidth=10, edgecolor="#eee")
plt.show()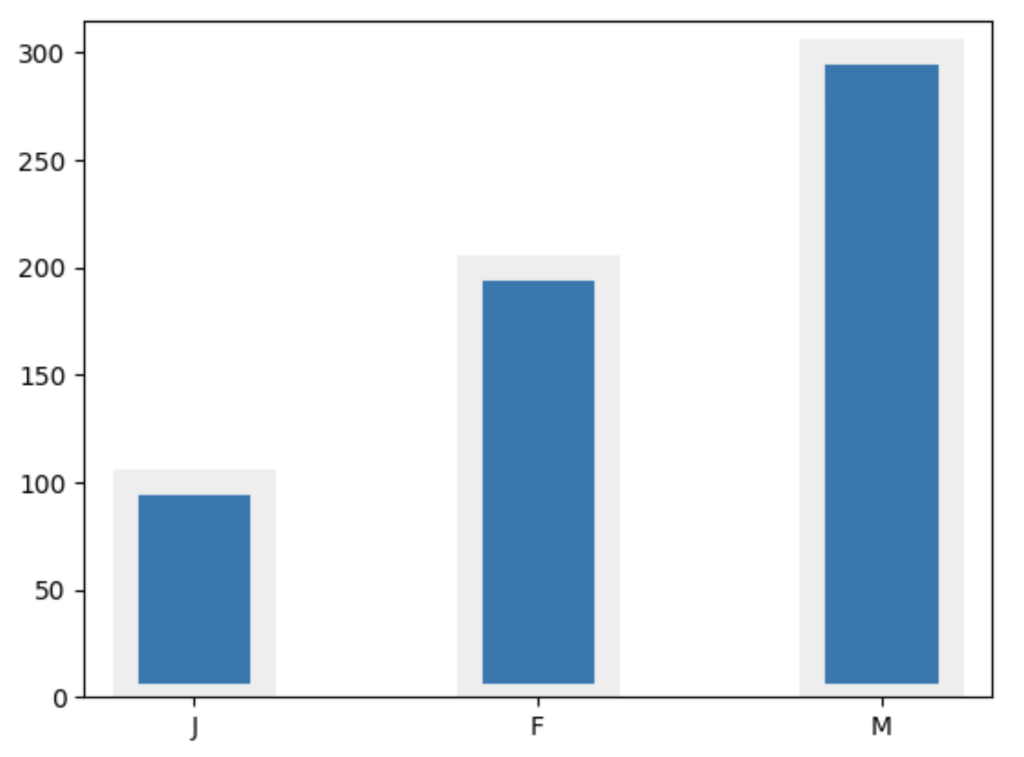
PythonのMatplotlibで折れ線グラフを作成する方法
続いては折れ線グラフです。
plotという一次関数でも使用したメソッドを使うことで折れ線グラフが作成できます。
plotは第一引数にxの値、第二引数にyの値、第三引数にcというキーワードで線の色、第四引数にlinewidthというキーワードで線の太さ、第五引数にmarkerというキーワードでプロットの形を指定します。
import matplotlib.pyplot as plt
x = ["J","F","M","A"]
y = [100,150,80,120]
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# x軸、y軸、線の形、線の色、線の太さ、点の形
ax.plot(x, y, "-", c="#666", linewidth=1, marker="+")
plt.show()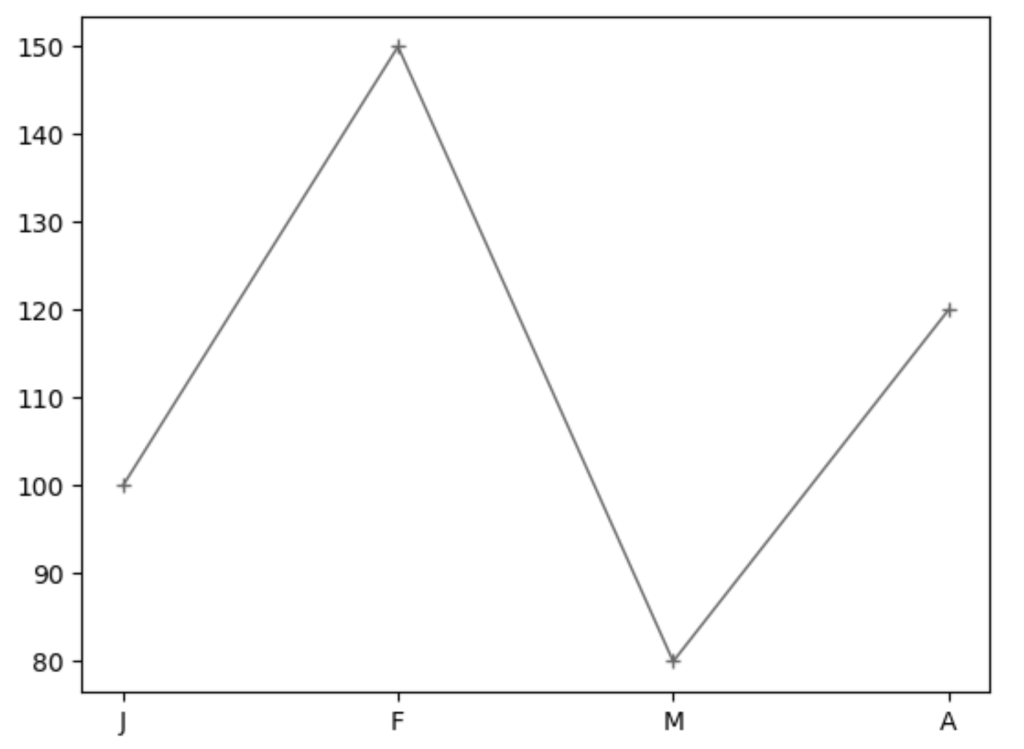
PythonのMatplotlibで円グラフを作成する方法
続いて円グラフの作成方法です。
円グラフはpieというメソッドを使用します。
第一引数に値、第二引数で値に対するラベル名、第三引数が値に対する色、第四引数にcounterclockというキーワードで値の並べる順番、第五引数にstartangleというキーワードで開始角度を指定します。
また円グラフは表示するエリアによって綺麗な正円にならず潰れた円形になることがあります。
それを防ぐためにaxisという補正メソッドを引数equalで実行することも併せて覚えておきましょう。
import matplotlib.pyplot as plt
label = ["AAA","BBB","CCC"]
x = [10,20,40]
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# 値、ラベル、色、Trueで時計回り、開始角度
ax.pie(x, labels=label, colors=['red', 'blue', 'green'], counterclock=False, startangle=90)
# 表示補正
ax.axis("equal")
plt.show()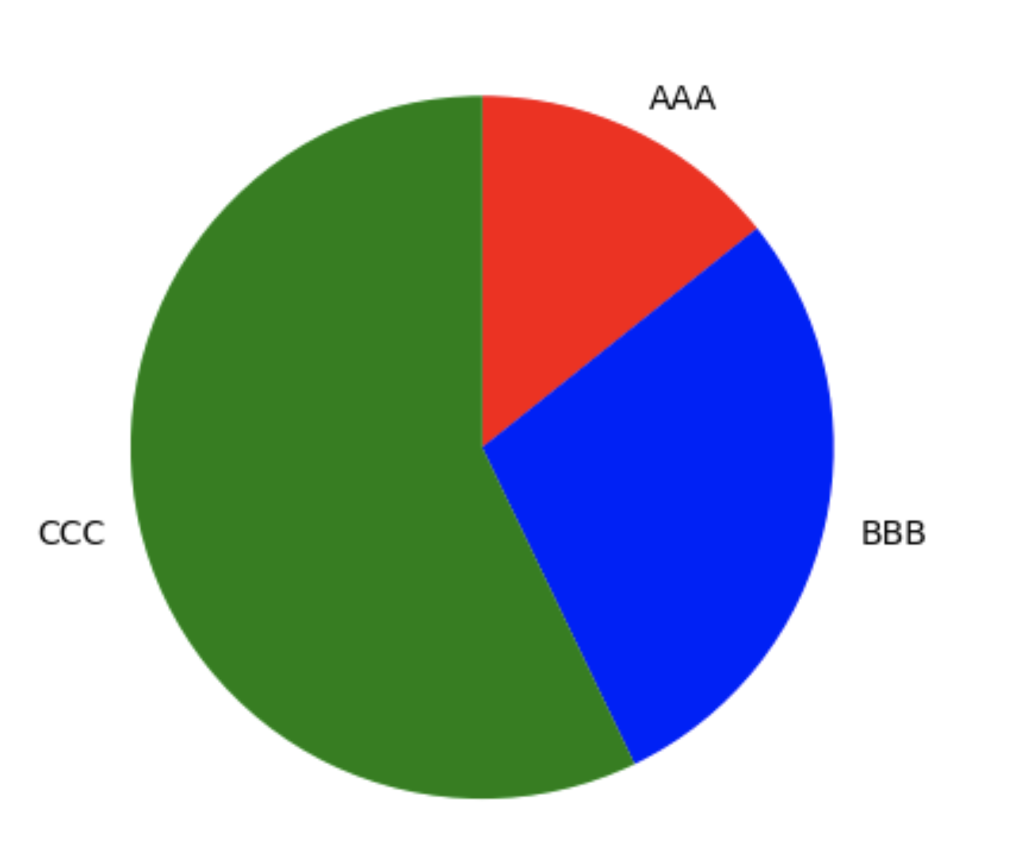
PythonのMatplotlibでヒストグラムを作成する方法
値の正規分布や偏りを確認するために使用されるヒストグラムも作成できます。
ヒストグラムは大量のデータが必要なので、今回はサンプルデータの用意にNumpyライブラリを使用します。
ヒストグラムはhistというメソッドがあり、第一引数に値、第二引数にbinsというキーワードで棒の数、第三引数にcolorというキーワードで棒の色、第四引数にecというキーワードで枠線の色を指定します。
pip install Numpyimport matplotlib.pyplot as plt
import numpy
# 平均値0, 標準偏差(ばらつき具合)10, 要素数100個
x = numpy.random.normal(0, 10, 100)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# x, 分割の数、棒の色、枠線の色
ax.hist(x, bins=20, color="#666", ec="#000")
plt.show()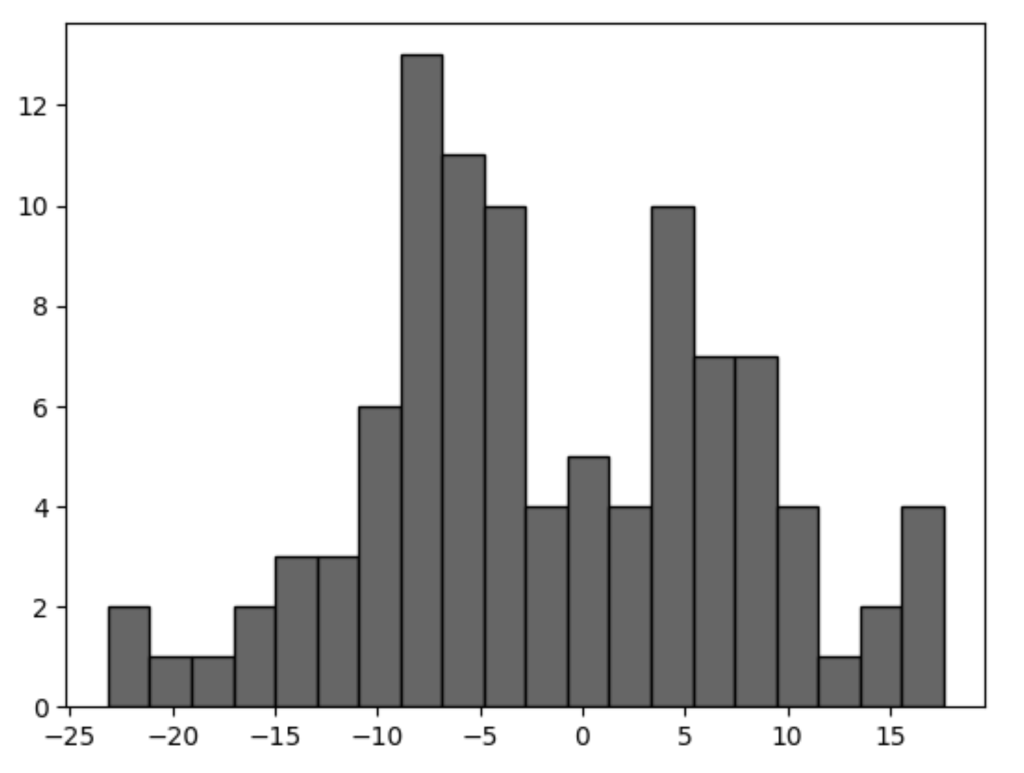
ちなみにヒストグラムの中で特定の値がバラツキの中でどれくらいの位置にいるかを調べる方法があります。
scipyというサードパーティ製のライブラリをインストールします。
!pip install scipy例えば身長のバラつきをヒストグラムにするとします。
データは平均値を165cmにして標準偏差を6にしたランダムな100個のデータをnumpyライブラリを使って用意しました。
import matplotlib.pyplot as plt
import numpy
# 平均値165, 標準偏差(ばらつき具合)6, 要素数100個
x = numpy.random.normal(165, 6, 100)
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.hist(x, bins=20, color="#666", ec="#000")
plt.show()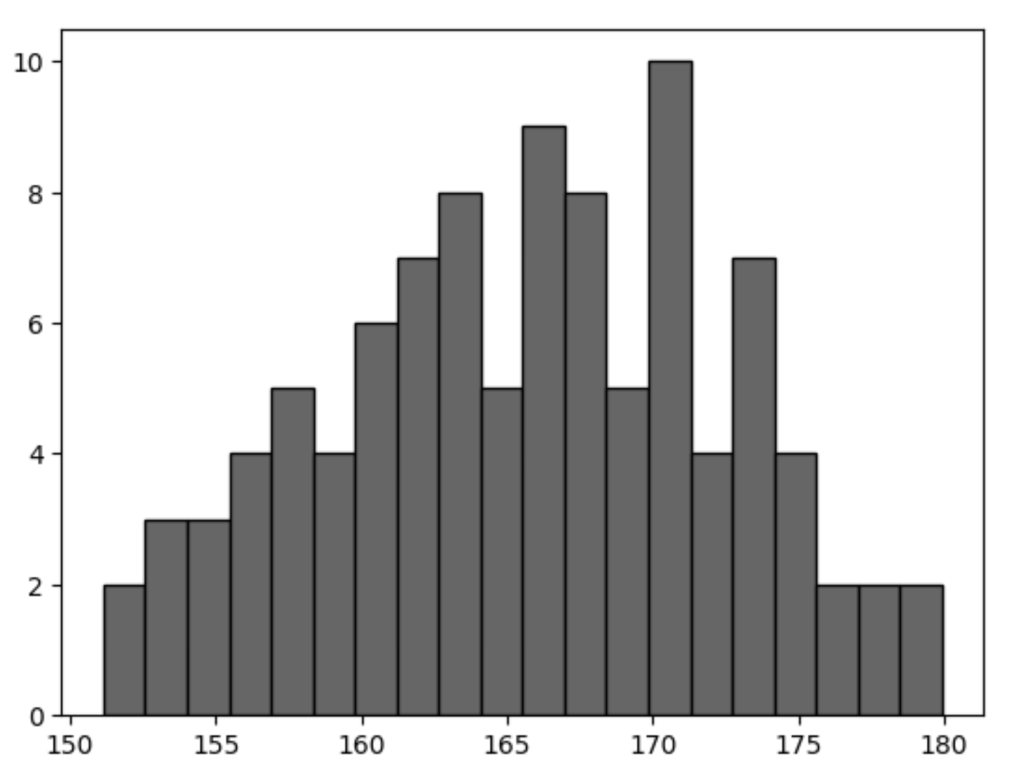
例えば身長170cmの人は上図のグラフの中でどこら辺の位置にいて全体から見た何%に当たるのかを調べたいとします。
from scipy.stats import norm
mean = 165
std = 6
value = 170
# 調べたい値、平均値、標準偏差(ばらつき)
cdf = norm.cdf(x=value, loc=mean, scale=std)
print(f"{value}cmは下から{round(cdf * 100)}%です")scipyにはnormというクラスがあり、normクラスにはcdfメソッドというものがあります。
第一引数に調べたい値、第二引数にデータにおける平均値、第三匹すうにデータにおける標準偏差を指定すると、第一引数に入れた170cmがどれくらいの位置にいるかを数字にして計算してくれます。

通常は下からの位置を特定するのですが平均値165cmを上回る値については上からの位置の方が自然ですよね。
その場合は以下のような計算式にします。
from scipy.stats import norm
mean = 165
std = 6
value = 170
cdf = norm.cdf(x=value, loc=mean, scale=std)
# ここを修正
print(f"{value}cmは上から{round((1 - cdf) * 100)}%です")
先ほど下から80%だったので上からの位置は20%という結果になりました。
平均値と比べて上からの位置か下からの位置かは考えられると良いでしょう。
またnormクラスにはcdfメソッドで特定した位置を検算するメソッドであるppfというものがあります。
上から20%の身長は何cmか?ということを調べれられるわけです。
from scipy.stats import norm
# ここから変更
mean = 165
std = 6
cdf = 0.8
# 位置、平均値、標準偏差
ppf = norm.ppf(q=per, loc=mean, scale=std)
print(f"下から{cdf * 100}%の身長は{round(ppf)}cmです")ppfメソッドは第一引数にcdfの値、第二引数にデータの平均値、大さん引数にデータの標準偏差を入れると第一引数に入れた0.8(下から80%)が何cmになるのか計算してくれます。

先ほどやったようなcdfを上からの位置で計算していた場合は以下のようにします。
from scipy.stats import norm
mean = 165
std = 6
cdf = 0.8
# ここから変更
per = 1 - per
ppf = norm.ppf(q=(1 - per), loc=mean, scale=std)
print(f"上から{round((per * 100))}%の身長は{round(ppf)}cmです")
ちなみにcdfやppfを使う代表例として学校の偏差値があります。
偏差値は平均値50で標準偏差10と固定の値になっているのでヒストグラムがなくても、「偏差値60が上から何%に位置するか?」「上から20%に入るには偏差値をいくつにするべきか?」といった問いを計算して出すことができるのです。
まずはcdfからです、リストのdataというものに偏差値を45,55,60,65の4種類で用意していて、それぞれ全体の中でどの位置にあるのか計算してみました。
from scipy.stats import norm
# ここから変更
data = [45, 55, 60, 65]
mean = 50
std = 10
for d in data:
cdf = norm.cdf(x=d, loc=mean, scale=std)
print(f"偏差値{d}は上から{round((1-cdf) * 100)}%です")
続いてppfを使って検算をします。
先ほど計算したcdfはどの偏差値のことになるのか計算してみました。
from scipy.stats import norm
# ここから変更
per = [0.07, 0.16, 0.31, 0.69]
mean = 50
std = 10
for p in per:
ppf = norm.ppf(q=(1-p), loc=mean, scale=std)
print(f"上から{round(p * 100)}%に入るには偏差値{round(ppf)}を目指すことになります")
Pythonのmatplotlibを使って箱ひげ図を作る方法
ヒストグラムと同じように「データのばらつき」を確認するためのグラフに箱ひげ図というものもあります。
箱ひげ図はboxplotというメソッドを実行するだけで作成できます。
pip install matplotlib
pip install pandas
pip install japanize_matplotlibimport pandas
import matplotlib.pyplot as plt
import japanize_matplotlib
data = {
"英語": [60,70,80,90,56],
"数学": [54,86,45,98,76],
"国語": [87,54,98,43,66],
}
df = pandas.DataFrame(data)
df.boxplot()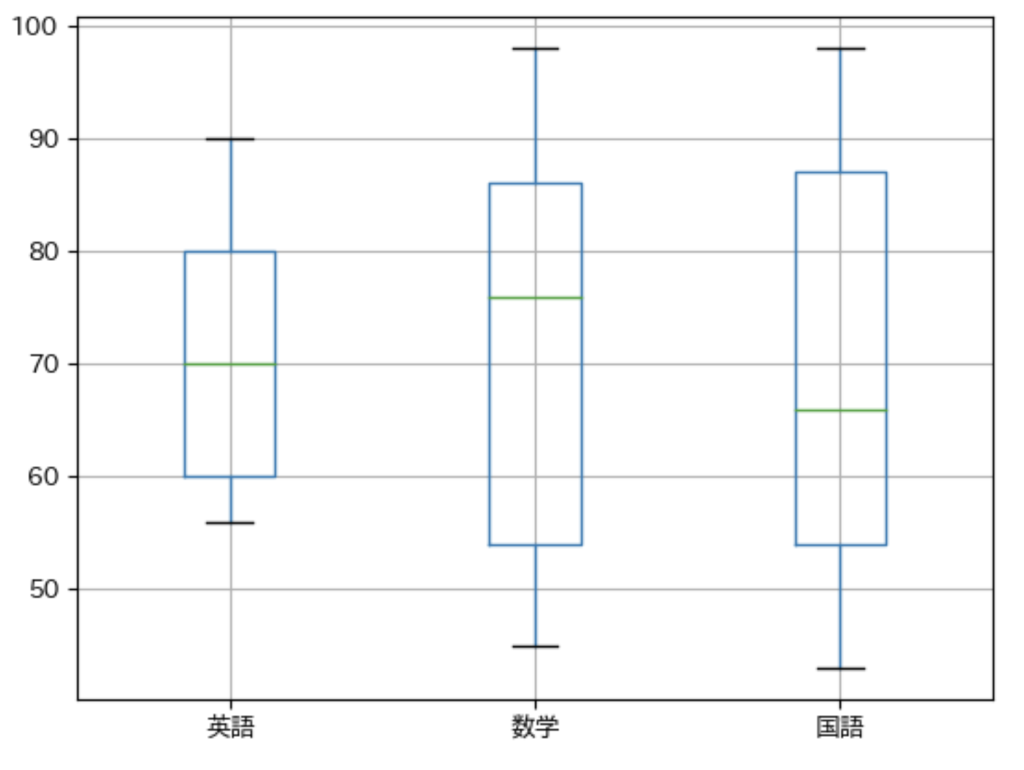
それぞれの箱がデータの範囲になっていて箱が大きくなればなるほど「最低値と最大値の格差が大きい」ことを表します。
また上図で緑線が中央値になっています。
中央値はpandasのmedianというメソッドでも数値を計算することができます。
import pandas
import matplotlib.pyplot as plt
import japanize_matplotlib
data = {
"英語": [60,70,80,90,56],
"数学": [54,86,45,98,76],
"国語": [87,54,98,43,66],
}
df = pandas.DataFrame(data)
df.boxplot()
# ここを追加
print(df.median())
